Subgraph sorting

We have a graph:

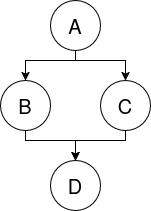
We sort this graph topologically into a one-dimensional sequence:

A, B, C, D

The exact sorting order is determined by inspecting the contents of these nodes (not shown here), and doing some kind of unspecified complex comparison on those contents. As this is a topological sort, the comparison is essentially the secondary sorting criterium; the primary sorting criterium is whatever preserves the graph order of the nodes (that is, an ancestor always comes before the node that it is an ancestor of). Crucially, this means that nodes in different branches are compared to each other.

The resulting sorting order is stored in a database, in some sort of order representation. The exact representation is undefined; which representation would work best here, is part of the problem being posed.

Now, the graph is expanded with a newly discovered side branch, introducing two new nodes, E and F:

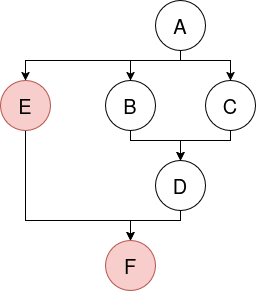
The new node E now participates in the sorting alongside B, C, and D - we know that E must come after A and before F, because of the ancestor relationships, but we do not know how exactly its ordering position in the sequence relates to the other three nodes, without actually doing the comparison against them.

The problem: the existing order (A, B, C, D) must be updated in the database, such that E and F also become part of the ordered sequence. The constraints are:

• The process may not load A, B, C and D into memory all at once. Loading them into memory on-demand is acceptable, as long as the performance cost is not too high, and there is never more than one node loaded into memory at once. Assume a standard file-backed key/value store as the database.
• The process should avoid rewriting the entry in the database for all of the existing nodes A, B, C and D. Some rewriting is acceptable, but having to rewrite every other participating node constitutes a performance problem.
• The outcome must be deterministically identical to what the outcome would have been if the graph had been fully known upfront, and sorted topologically, all at once in memory.

You may choose any internal representation in the database, and any sorting mechanism, as long as it fits within the above constraints.